2022. 2. 20. 18:06ㆍ고체역학
- Stress : 단위 면적당 작용하는 하중
1. Normal Stress (수직 응력)
$$\sigma = \frac{F}{A} [N/m^{2} = Pa]$$
Normal Stress는 작용면에 수직으로 가해지는는 힘을 지칭하고, 이때 면에서 나오는 방향이 +방향이다.
하중을 해석할 때 부재에 여러 힘이 작용할 경우 하중이 변하는 부분을 모두 끊어서 해석하면 된다.
이때 부재의 각 부분에서는 Force나 Moment가 0이 아닌 값으로 나올 수 있지만, 전체적으로 평형을 이루고 있기 때문에 움직임이 없이 정적으로 존재할 수 있다.

2. Shear Stress (전단 응력)
$$\tau = \frac{V}{A} [N/m^{2} = Pa]$$
Shear Stress는 작용면과 평행하게 가해지는 힘을 지칭하고, 이때 내력은 ->방향을 기준으로 아래방향이 +방향이다.
평형을 유지하는 물체에서는 국소적으로 봤을 때 아래와 같이 우측면에서 위로 향하는 Shear Stress가 +이다.
마찬가지로 Shear Strain($\gamma$)이 90도보다 작아지는 방향을 +로 정하였다.

- 안전계수 (n : Factor of Safety : F.S.)
물체에 가해질 수 있는 하중을 고려했을 때 얼마나 더 단단히 만들어야 할지에 대한 계수이고 그 값은 항상 1보다 커야한다.
$$n=F.S.=\frac{F_{fail}}{F_{allow}} = \frac{\sigma_{fail}}{\sigma_{allow}} = \frac{\tau_{fail}}{\tau_{allow}}> 1$$
- Strain : 물체가 원래의 길이보다 얼마나 길어졌는지에 대한 비율
1. Normal Strain
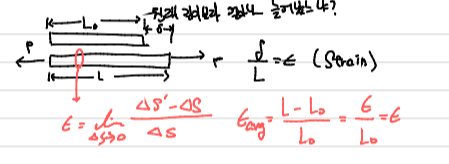
$$\epsilon = \frac{L-L_0}{L}=\frac{\delta}{L}$$
Normal Strain은 Normal Stress에 의해 변화하는 길이를 의미한다. 이때 Tension에 의해 늘어나는 것을 +로 한다.
2. Shear Strain
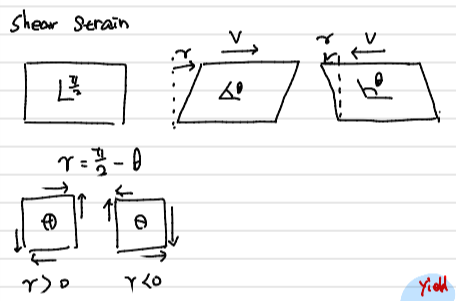
$$\gamma = \frac{\pi}{2}-\theta$$
Shear Strain은 Shear Stress에 의해 변화하는 길이를 의미한다. 이때 위의 그림에서와 같이 사이각이90도 보다 작아지는 경우를 +로 한다.
* Hooke's law
후크의 법칙은 Stress와 Strain사이의 관계를 나타낸 식이다. 그 식은 아래와 같다.
$$\sigma = \epsilon E$$
$$\tau = \gamma G$$
이는 아래와 같이 쓸 수 있다.
$$\frac{P}{A}=E\frac{\delta}{L}$$
$$F=-kx$$
$$k = \frac{EA}{L}$$
* Strain Stress Diagram

위는 Ductile Material의 Stress-Strain Diagram의 그래프이다. 그래프에 대한 설명은 아래와 같다.
처음Elastic Region에서는 Stress가 증가함에 따라서 strain값이 선형적으로 증가하지만, Yielding Stress($\sigma_y$)이상의 Stress에 대해서는 더이상 Stress가 증가하지 않고 길이만 증가한다.
이후에는 Stress가 증가함에 따라 길이가 비 선형적으로 증가하는 Region이 있다.
이때 가했던 Stress를 줄이면 원래의 길이로 돌아오지는 않지만, 물질의 Elastic Modulus값 대로 선형적으로 감소하게된다. 이 상태에서는 어느정도의 Stress를 받아도 항복이 일어나지 않도록 Yielding에 대한 내성을 강화했기 때문에 큰 Stress에 대한 내성을 갖추게 되어, 이를 Stress Hardening Region이라고 한다.
하지만 Stress Hardening을 한 이후에는 부재의 Distorsion Energy의 총량$U=\frac{1}{2}\sigma \epsilon V$가 줄어들게 되어 파단에 대해서는 내성이 낮아지게 된다.
이후 가장 큰 Stress인 Ultimate Stress($\sigma-{ult}$)가 나타나고 가해지는 Stress가 작아지다가 부러지는 Necking이 발생하게 된다.
하지만 Ultimate Stress이후에 실제로 물체가 받는 Stress는 항상 증가한다. 그 이유는 Yield에 의해 Yield이 일어나고 있는 부분의 단면적 A가 계속 작아지기 때문에 ($\sigma = \frac{P}{A}$)에 의해 Stress는 커지게 된다. 그래서
해당 Stress에 대한 그래프는 위의 그래프에서 계속 증가하는 푸른 선으로 확인할 수 있고, 이 그래프를 True Stress- Strain Diagram이라고 한다.
Brittle Material에 대한 Stress-Strain Diagram은 위의 그래프와 유사하게 Elastic Region이 존재하지만 Yield이 거의 없이 파단되어 선형적인 그래프를 나타낸다.
- Ductile Material과 Brittle Material
| Ductile Mateial | Brittle Material | |
| 종류 | 구조용 강, 철, 합금 | 유리, 콘크리트, 분필, 알루미늄 |
| 특징 | - Elastic Region, Yield, Plastic Region등이 뚜렷이 구분된다. - 충격이나 외력에 의해 바로 파괴되는 것이 아니라 흡수할 수 있어 설계시 재료로 많이 사용된다. - Slipping에 의해 Yielding등이 발생하기 때문에 $\tau_{shear} = \frac{\sigma_y}{2}$ 가 작용할 때 항복이 일어난다. |
- 보통은 Plastic Region등이 보이지 않고 Elastic Region에서 파단이 되는 모습을 볼 수 있다. |
- Poisson's Ratio
이전까지는 힘을 가했을 때 힘을 가해준 축의 길이변화만 생긴다고 가정했지만, 실제로는 그렇지 않다. x축방향으로 Stress$\sigma_x$가 작용 할 때 $\epsilon_x$뿐만 아니라 $\epsilon_y$, $\epsilon_z$의 변화도 생기고 그 비율에 대한 계수를 $\nu$라고 하고 이는 0<=$\nu$<=0.5 의 값을 갖는다.
$$\nu = -\frac{\epsilon_{lat}}{\epsilon_{long}} =\frac{하중을 가하지 않은 축 방향의 변형율}{하중을 가한 축 방향의 변형율}$$
이때 Poissons's Ratio를 적용한 일반화된 Hooke's Law는 아래와 같고,
$$\epsilon_x = \frac{1}{E} [\sigma_x - \nu (\sigma_y + \sigma_z)]$$
이 식은 Plane Pure Shear($\tau_{xy}, \gamma_{xy}$)가 작용하는 경우 $\sigma_x = \tau, \sigma_y = -\tau, \sigma_z = 0, \epsilon_x = \frac{\gamma_{xy}}{2}$ 에 의해
$$ \epsilon_x = \frac{\gamma_{xy}}{2} = \frac{\tau_{xy}(1+\nu)}{E} = \frac{\gamma_{xy} G(1+\nu)}{E}$$
이다. 이 식을 정리하면 E와 G의 관계식이 아래와 같이 나오게 된다.
$$G = \frac{E}{2(1+\nu)}$$
'고체역학' 카테고리의 다른 글
| 고체역학 Shear Flow, Bending (0) | 2022.02.24 |
|---|---|
| 고체역학 Torsion (0) | 2022.02.22 |
| 고체역학 Axial Load (0) | 2022.02.21 |
| 고체역학 Intro (0) | 2022.02.20 |