2022. 2. 24. 16:08ㆍ고체역학
- Shear Flow
얇은 박막으로 된 물체에 Torsion이나 Shear Force에 의해 전단응력(Shear Stress)가 발생할 경우, 부재의 단면에는 전단 류 (Shear Flow)가 발생한다. Shear Flow를 구하는 방법은 다음과 같다.
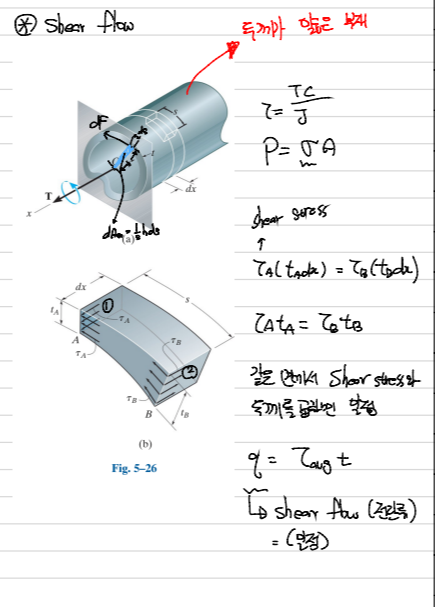
위의 그림과 같이 얇은 박판으로 되어있는 부재가 있다고 가정하자. 중심에서 박판의 중심까지의 거리는 t, 박판의 두께는 $t_i$ 토크에 의해 박판을 dx로 잘랐을 때 임의의 박판의 한 점에 작용하는 힘을 dF라고 하면 dF = $\sigma$ dA = $\tau_A t_A$dx = $\tau_B t_B$dx 로 나타낼 수 있다. 식을 다시 정리하면 아래와 같다.
$$q(Shear Flow) = \tau_A t_A = \tau_B t_B = \tau_{avg} t$$
이를 이용하면 $dF = \sigma dA = \tau_{avg} t ds = q ds$로 표현할 수 있다. (이떄 ds는 임의의 단면의 가로길이)
이때 ds를 양변에 나누어 주면,
$$q = \frac{dF}{ds}$$
Shear Flow는 위의 식에서 단위길이당 하중을 의미한다는 것을 알 수 있다.
- Hollow Shaft 의 Polar Moment of Inertia
$$dF = \tau_{avg} t ds$$
$$dT = dF*h = h \tau_{avg} t ds$$
$$\int dT = T = \oint h \tau_{avg} t ds = t \tau_{avg} \oint h ds = 2 \tau_{avg} t Am$$
아주 작은 ds에 대해서는 $h ds$가 위의 그림에서 파란색으로 표시된 것 처럼 부채꼴의 면적과 같기 때문에 $\oint h ds = S = \frac{rl}{2}$에 의해서 2Am (Am은 점선으로 안쪽 부재 내부의 넓이)으로 표현할 수 있다. 따라서 아래와 같은 식을 도출 할 수 있다.
$$\tau_{avg} = \frac{T}{2tAm}$$
$$q = \frac{T}{2Am}$$
- Angle of Twist
앞에서 Angle of Twist는 $\phi = \frac{TL}{JG}$라고 공부 한 바 있다. 앞에서 배운 Shear Flow를 이용하여 Angle of Twist를 다르게 도출 해볼 수 있는데.
$$\frac{dU}{dV} = \frac{\tau \gamma}{2} = \frac{\tau^2}{2G}$$
$$dU = \frac{\tau^2}{2G} dV = \frac{\tau^2}{2G} t ds dx = \frac{\tau^2 t^2}{2G} \frac{ds}{t} dx= \frac{q^2}{2G} \frac{ds}{t} dx$$
$$U = \int dU = \frac{q^2}{2G} \int_{0}^{L} dx \oint \frac{ds}{t} = \frac{q^2 L}{2G} \oint \frac{ds}{t}$$
$q = \frac{T}{2Am}$ 이므로
$$U = \frac{T^2 L}{8G Am^2} \oint \frac{ds}{t} = \frac{T \phi}{2}$$
한편 $\phi = \frac{TL}{JG}$로 알려져 있기 때문에 위의 식은 다시
$$U = \frac{T^2 L }{8G Am^2} \oint \frac{ds}{t} = \frac{T^2 L}{2JG}$$
정리하면 J는 아래와 같이 나온다.
$$J = \frac{4Am^2}{\oint \frac{ds}{t}}$$
- Bending (굽힘)
Bending은 Moment의 일종이다. Torsion Moment가 Shear Stress를 만드는 Force라면 Bending Moment는 Normal Stress를 만드는 Force라고 할 수 있다.
Bending이 어떻게 Shaft에 작용하는 지 공부하기 전에 Beam을 지지하는 3가지 기본적인 구조를 알아보면 아래와 같다.
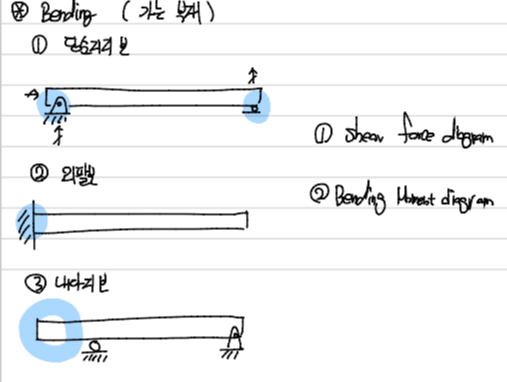
첫 번째는 단순지지보로 한쪽에는 Pin 고정 나머지 한쪽 끝에는 Roller로 지지하고있는 구조이다.
두 번째는 외팔 보로 한쪽 끝에만 Fixed end로 되어있는 구조이다.
세 번째는 내다지 보로 한쪽 끝에는 Pin고정 그리고 중간부분에 Roller로 지지하고 있는 구조이다.
다음으로는 Beam에서의 Sign Convention에 대해서 알아볼 필요가 있다.
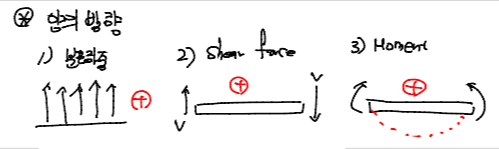
1) 분포하중이다. Beam해석에서 외력으로 분포하중이 나왔을 때는 위로 향하는 하중을 +하중으로 생각하면 된다.
2) Shear Force이다. Beam해석에서 Internal Shear Force의 양의 방향은 우측 면에서는 아랫방향, 죄측 면에서는 윗 방향이 +방향이다.
3) Moment이다. 모멘트의 경우 Beam을 아래로 볼록하게 휘게만드는 방향이 +방향이다. 그래서 우측면에선 C.C.W 좌측 면에서는 C.W이다.
Beam에 다양한 하중이 작용할 때 임의의 점에서 어느 정도의 Moment가 작용하는지 쉽게 알기 위해서는 Bending Moment Diagram을 그려보는게 효과적일 수 있다.
Bending Moment Diagram을 그리는 순서는
1) Free Body Diagram을 그리고 Beam에 작용하는 모든 힘을 구한다.
2) Shear Force Diagram(이하 S.F.D.)을 그린다.
3) S.F.D.을 참고하여 Bending Moment Diagram(이하 B.M.D.)을 그린다.
S.F.D.을 그리는 이유는 $\frac{dM}{dx} [Nm/m]= V[N]$이므로 Shear Force의 크기가 B.M.D.의 기울기 이기 때문이다.
S.F.D을 그리는 방법은 왼쪽에서부터 x = 0이라고 가정한다면, 위로향하는 집중하중이나 분포하중이 있으면 양의 방향으로 올려주면 된다. 이때 분포하중의 경우($\frac{dV}{dx} [N/m]= w{N/m}$)이므로, Unitstep Function이라면 S.F.D.에서는 분포하중의 크기를 기울기로 하는 1차함수로 나타낸다. 1차함수의 분포하중에서도 마찬가지로 해당 분포하중을 적분해준 2차함수로 S.F.D.이 나온다. 만약 집중하중이 있을 경우 S.F.D.을 불연속하게 증가하거나 감소하도록 그려주면 된다.
S.F.D.에서 External Moment는 무시하고 그려주어도 상관없다. 그 이유는 앞에서 말했듯이 Bending Moment를 미분해주면 Shear Force가 되는데 이때 External Moment는 Bending Moment식에서 상수로 들어간다. 따라서 미분해주면 0이되기 때문에 Free Body Diagram에서 External Moment가 있다면 S.F.D.을 그릴때 무시해 주면 된다.
B.M.D.을 그리는 방법은 S.F.D.를 그리는 방법과 유사하다. S.F.D.의 적분이 B.M.D이므로 그 점을 염두에 두고 그리면 되고, External Moment가 존재할 경우 C.W를 +로 설정하여 그려주면 된다. 이 때 Internal Moment때와 달리 C.W일 때 +인 이유는 C.W인 External Moment가 C.C.W의 Internal Moment를 만들어 주기 때문이다.
- w, V, M사이의 상관관계
위에서 말했듯이 M의 미분이 V이고,V의 미분이 w이다. 이를 증명해 보려고 한다.
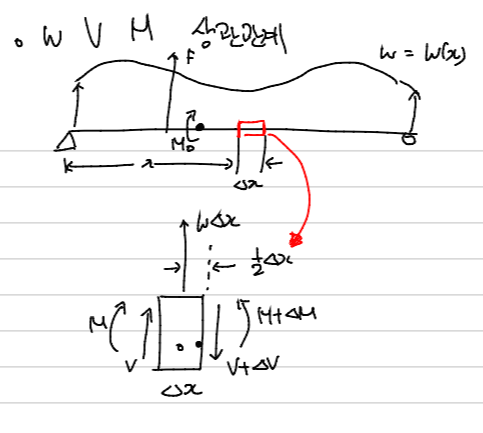
위의 그림과 같은 하중이 가해지고 있는 단순지지보를 예를 들어보면, 임의의 한 부분을 $\Delta x$만큼 뗴어와서 그 부분에 작용하고 있는 하중을 그려본 모습이다.
Equation of Equilibrium을 사용하여 식을 세워보면
1) $\sum F_y =0$
$$\sum F_y = 0 = V - V - \Delta V+ w\Delta x$$
$$\Delta V = w\Delta x$$
$$\frac{\Delta V}{\Delta x} = w$$
$$\lim_{\Delta x \to \infty} \frac{\Delta V}{\Delta x} = \frac{dV}{dx} = w$$
2) $\sum M = 0$
$$\sum M = 0 = - M - V\Delta x -w\Delta x (\frac{\Delta x}{2}) + M + \Delta M$$
이때 $\Delta x^2$은 작은수*작은수 이기 때문에 다른 항에 비해서 무시할 수 있을만큼 작은 수이다. 따라서 근사적으로 없애도 상관 없으므로,
$$\Delta M = V\Delta x$$
$$\frac{\Delta M}{\Delta x} = V$$
$$\lim_{\Delta x \to \infty} \frac{\Delta M}{\Delta x} = V$$
정리하면,
$$\frac{\Delta V}{\Delta x} = w, \frac{\Delta M}{\Delta x} = V$$
- 만약 외력으로 작용하는 힘이 집중하중 F일 경우
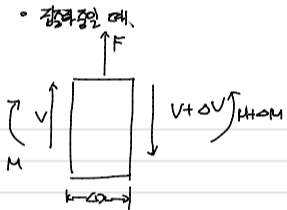
1) $\sum F_y = 0$
$$0 = V + F - V - \Delta V$$
$$\Delta V = F$$
따라서 하중 F가 S.F.D.의 기울기로 작용하는게 아니라 크기로서 작용한다.
2) $\sum M = 0$
$$0 = - M - V\Delta x -\frac{F\Delta x}{2} + M + \Delta M$$
$$\Delta M = V\Delta x + \frac{F\Delta x}{2}$$
이때 우리가 설정한 부재의 임의의 부분 $\Delta x$는 아주 작은 크기의 부분이다. 이 값을 더욱 작게해서 새로운 $\Delta x$ 을 극한을 취하더라도 집중하중 F는 그보다 더 작은 부분에서 작용하는 위치정보만 존재하는 하중값이다. 따라서 이때의 $\Delta x$는 무한소이므로 집중하중 F는 B.M.D.에 영향을 미치지 않는다.
- 만약 외력으로 집중 모멘트($M_o$)가 작용한다면
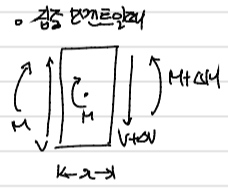
1) $\sum F_y = 0$
$$0 = V - V - \Delta V$$
$$\Delta V = 0$$
2) $\sum M = 0$
$$0 = -M-V\Delta x - M_o + M + \Delta M$$
$\Delta x$를 0 으로 보내면,
$$\Delta M = M_o$$
이다.
- Bending Deformation of Shaft
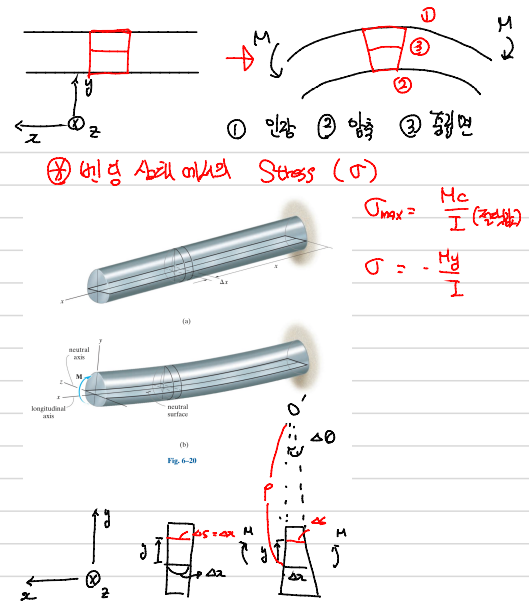
Shaft에 Bending Moment가 가해지면 위의 그림과 같이 중립면의 길이는 원래와 같고 압축면의 길이는 짧아지고 인장면의 길이는 길어진다.
위의 그림을 보면 양의 Bending Moment가 작용한다. 이때 곡률 반지름을의 중심부터 중립면 까지의 거리를 $\rho$라고하고 중립축 에서 위로 y인 곳의 길이를 $\Delta S$ 라고 하자. 이때 $\Delta S$의 Strain을 구해보면
$$\epsilon = \lim_{\Delta S \to 0} \frac{\Delta S'-\Delta S}{\Delta S} = \frac{(\rho - y)\Delta \theta - \rho \Delta \theta}{\rho \Delta \theta}$$
$$\epsilon = -\frac{y\Delta \theta}{\rho \Delta \theta}$$
단면에서 중심축에서 가장 먼곳까지의 길이를 c라고 한다면 위의 식은 아래와 같이 쓸 수 있다.
$$\epsilon = -\frac{y}{c} \epsilon_{max}$$
이 식은 Hooke's law에 의해
$$\sigma = -\frac{y}{c} \sigma_{max}$$
라고 쓸 수 있다. Bending Moment에 의해 부재가 움직여서 평형을 유지하고 있다면, 임의의 단면을 잘랐을 때 단면에서 작용하고 있는 Normal Stress의 Resultant(합력)은 0 이 되어야 하므로 이를 식으로 적어보면,
$$F_R = \int_{A} dF = \int_{A} \sigma dA = \int_{A} -\frac{y}{c} \sigma_{max} dA = 0$$
$$\int_{A} y dA = 0$$
위의 식은 면적에 거리를 곱한값들의 총 합이다. 중심축을 기준으로 위쪽은 y>0 , 아래쪽은 y<0 이기 때문에총합이 0이 될 수 있고 그 축을 중심축이라고 한다.
Moment와 Stress사이의 관계식은 $dM = y dF$이다. 양변을 적분해보면,
$$M = \int y dF = \int y \sigma dA = \int -\frac{y^2}{\rho} dA$$
$\int y^2 dA = I$는 Moment of Inertia이다. 따라서, 식을 $\sigma$에 대해 정리하면 아래와 같고,
$$\sigma = -\frac{M\ rho}{I}$$
이 식은 Bending Moment가 작용했을 때 단면의 임의의 지점에서 Normal Stress를 구할 수 있는 'Flexure Formular이다.
- Center of Mass
사각형이나 원형이 아닌 부재의 CoM을 구하는 방법은, 그 부재를 간단한 부재로 나누어서 구할 수 있다.
각 부재의 CoM와 Ref축사이의 거리를 $\bar y_i$, 면적을 $A_i$라고 하면 식은 아래와 같다.
$$\frac{\sum_{i = 0}^n \bar y_i A_i}{\sum_{i = 0}^n A_i}$$
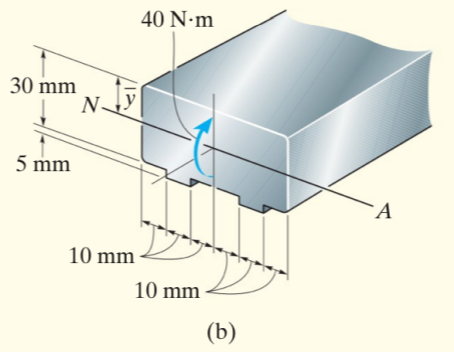
위의 부재 같은 경우 아래 다리 부분과 윗 부분으로 나누어서 계산하면 된다. Ref축 윗부재의 제일 위쪽으로 잡고 CoM를 계산하면,
$$\bar y_{tot} = \frac{0.015*0.03*0.06+2*0.0325*0.005*0.01}{0.03*0.06+2*0.005*0.01} = 0.01592 [m]$$
이 축이 Moment가 작용하고 있는Neutral Axis로서 Moment of Inertia 를 구할 때의 중심축으로 설정하여 $I' = I + Ad^2$을 이용하여 구하면 된다.
- Neutral Axis와 나란히 작용하지 않는 Moment
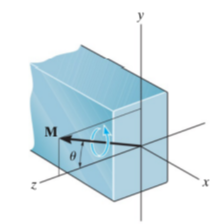
이런 식으로 힘이 작용할 경우 힘을 y, z축으로 각각 분해해서 $\sigma_x=$-\frac{My}{I}$공식을 이용하여 구한다.
$$\sigma_x = -\frac{M_zy}{I_z} - \frac{M_y(-z)}{I_y} = -\frac{M_zy}{I_z} + \frac{M_yz}{I_y}$$
이때 Neutral Axis는 $\sigma$값이 없는 0인 지점을 의미하므로 위의 식에서 $\sigma_x = 0$으로 하여 y에 대한 식으로 정리를 하게 되면 아래와 같이 일차함수로 나타난다.
$$y = \frac{M_yI_z}{M_zI_y} z$$
이때 $M_z = M\cos \theta, M_y = M\sin \theta$이므로, 위의 식에 대입하면
$$y = \frac{I_z}{I_y} \tan \theta z$$
임을 알 수 있다. 이 식에서 우리는 부재의 단면이 각 Axis에 Symmetric해야만 Neutral Axis의 방향 = Moment의 방향임을 확인 할 수 있다.
- Composite Beam
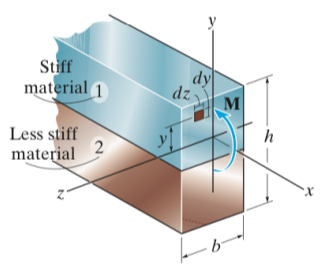
만약 부재가 위 그림처럼 두가지 이상의 물질로 구성되어 있다면(예를 들면 Bimetal), 같은 Bending Moment를 받아서 같은 정도만큼 구부러져도 받는 Stress값은 Hooke's law($\sigma = E\epsilon$)에 따라서 다르게 작용 할 것이다. 따라서 $\sigma$값이 불연속하므로 적분불가능하여 Bending Formular를 바로 적용할 수 없기 때문에 한 부재를 다른 부재와 같은 Elastic Modulus를 가진 등가의 크기의 부재로 바꾸어 계산해 주는 방법을 사용한다.
$$\epsilon = -\frac{y}{\rho} = -ky, (k = \frac{1}{\rho} = \frac{1}{곡률 반지름})$$
$$\sigma = E\epsilon \ -Eky$$
이 상황의 경우 Bending Moment에 의한 $\sigma$는 y에 따라서 달라진다.
$E_1 = nE_2$라고 가정할 경우 아래와 같은 식을 세울 수 있다.
$$\sigma_R = 0 = - \int_{A1} nE_2 ky dA - \int_{A2} E_2 ky dA$$
이때 앞 항의 n을 dA로 넣어서 부재의 표면적을 n배 넓혀주면 두 적분식을 합칠 수 있다. 다만 $\sigma$가 y에 따라서 달라지기 때문에 가로로 넓혀주거나 좁혀준다. 이후에는 같은 물질의 재료이기 때문에 Bending Formular를 사용할 수 있다. 다만 $\sigma = \frac{F}{A}$이므로 만약 면적을 줄였을 경우 원래 해당부분의 Stress보다 더 넓은 범위의 Stress를 압축해서 받고 있는 것이기 때문에 크기를 줄인만큼 Stress값도 줄여주어야 하고, 면적을 늘렸으 경우 원래 해당부분의 Stress값보다 적게 받고 있는 것이기 때문에 늘려주어야 한다. 이를 공식으로 세워보면 아래와 같다.
$$E_1b_1 = E_2b_2$$
만약 가로길이 $b_2$인 2번 부재를 1번부재로 바꾸었을 때, 등가인 길이 $b_1$을 알고싶다면 위 식은
$$b_1 = \frac{E_2}{E_1} b_2$$로 바꾸어 쓸 수 있다. 이때 $\frac{E_2}{E_1}$이 Transformation Coefficient(n)이 되고 이후 2번 부재영역에서 $\sigma'$값을 구하면, 그 값의 원래 크기는 아래와 같다.
$$\sigma = n\sigma'$$
'고체역학' 카테고리의 다른 글
| 고체역학 Torsion (0) | 2022.02.22 |
|---|---|
| 고체역학 Axial Load (0) | 2022.02.21 |
| 고체역학 Stress, Strain (0) | 2022.02.20 |
| 고체역학 Intro (0) | 2022.02.20 |